It turns out however that the set of rational numbers is infinite in a very different way from the set of irrational numbers. There are after all an infinite number of rational numbers and an infinite number of irrational numbers.

Rational And Irrational Numbers Explained With Examples And Non Examples And Pictures
Extending this argument further we get Note.

. How many real numbers there are in total. So the most irrational numbersthe Liouville numbershave the property that one can squeeze the approximation neighborhood with an arbitrarily large inverse power of q and still find an unbounded number of rational approximations p q. Between any two real numbers a and b there are an infinite number of real numbers.
How is this possible then if theres is an infinite amount of each. In the same sense that one can say that there are more real numbers than there are rationals or integers. Two irrational numbers may or may not have a least common multiple.
There are more algebraic numbers than rational numbers in the sense that the algebraic numbers form a proper superset of the rationals but Cantor showed that the set of algebraic numbers is countable. There are more irrational numbers than rational numbers per Cantor. In other words there are more irrational numbers than rational numbers.
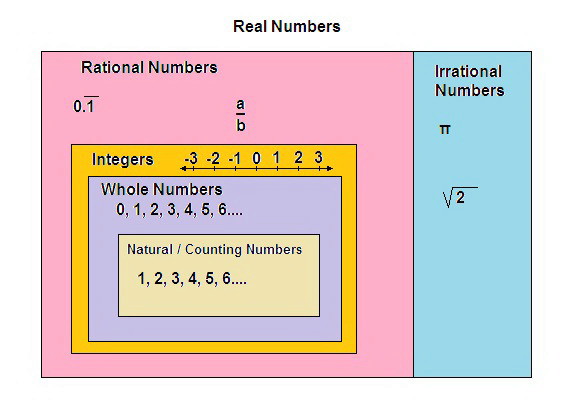
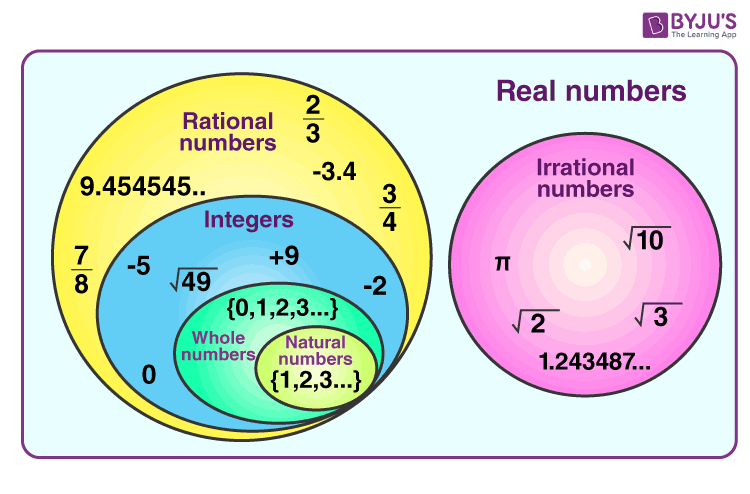
Real numbers are either rational or irrational. In fact the opposite is true as there are far more irrational numbers than rational. This means that you could say that there are more irrational numbers than there are rational.
The product of an irrational number and a rational number is irrational as long as the rational number is not 0. If it is assumed that every irrational number can be assigned to at least one counting numbers like the rationals then with such a list it is possible to find an irrational number that is not on. 2 its only capable of representing rational numbers No matter how you represent numbers Python or any other language on a realizable computer is only capable of representing a finite number of numbers.
Consider all numbers rational and irrational to be made up of an. Despite there being far more irrational numbers than rational numbers we have the properties that. Irrational numbers are not closed under addition subtraction multiplication and division.
See full answer below. Yes in the sense of cardinality. The higher the measure is for a number the easier it is to approximate that number with a rational number.
In the same sense there are as many but in particular no more rational numbers than there are integers. Rational numbers are countable. 1 but some corrections.
No there are not more rational numbers than irrational numbers. Lets say i have an irrational number c. ⅔ is an example of rational numbers whereas 2 is an irrational number.
Let that sink in. Edited Nov 15 2010 at 109. You can list and match up all rational numbers with irrational numbers this way.
If you were to pick a number between 0 and 1 with all possible numbers having the same chance of being picked the probability that you would get a rational number is effectively zero. This means there cannot be a one-to-one-correspondence with natural numbers and there are more irrational numbers than natural numbers and consequently more irrational numbers than rational numbers. So irrational numbers cannot be enumerated without missing at least one irrational number.
In a well defined sense most real numbers are irrational. There are fewer irrational numbers than rational numbers. They form what mathematicians call a countable infinity.
There we have it. Sometimes the symbol c is used denoting the cardinality of the continuum ie. Hence there are infinite rational numbers between 0 and 1.
Between any two distinct rational numbers is an irrational number. The same isnt true of the irrational numbers those. The rational numbers are countable but the irrationals are uncountable.
Every real number has a fixed base representation with at most a countable number of digits after the decimal point. Rn-crn There exists an irrational number that is not on this matching not equal to any of the crxs this irrational number can be made by multiplying c to another irrational number b. The answer here is that there are in fact far far more irrational numbers than there are rational numbers.
Without getting into the discussion that one of these infinities is infinitely greater than the other infinity we can get an idea as to how rare are the rational numbers in a space of real numbers. Assume we listed all the natural number with each theres a corresponding irrational number we can get a new irrational numbers by picking up the irrational on the diagonal of the existing list. But it seems there are always at least 1 more irrational number than all the rational numbers that we can list.
Real numbers are uncountable. What started as an unintuitive fact has now helped us understand just a bit more about infinities and their different sizes. One way to think about this is that between any two rational numbers there are an.
The sum of an irrational number and a rational number is irrational. But an irrational number cannot be written in the form of simple fractions. This is in contrast to rational numbers which.
Each of the obtained intervals at least adds one number to the count of rational numbers between 0 and 1. As we saw here the rational numbers those that can be written as fractions can be lined up one by one and labelled 1 2 3 4 etc. Follow this answer to receive notifications.
Because uncountably infinite sets are always larger than countably infinite sets we can finally conclude there are more irrational numbers than rational ones. A rational number is the one which can be represented in the form of PQ where P and Q are integers and Q 0. This is true despite the fact that all integers are rational and some rational numbers arent integers.
1 Python uses arbitrary-precision arithmetic I can make Python use continued fractions and voila.
Some Of The Coolest Numbers Are Irrational Mathnasium

Rational And Irrational Numbers Examples Songs Videos Worksheets Solutions Activities
0 Comments